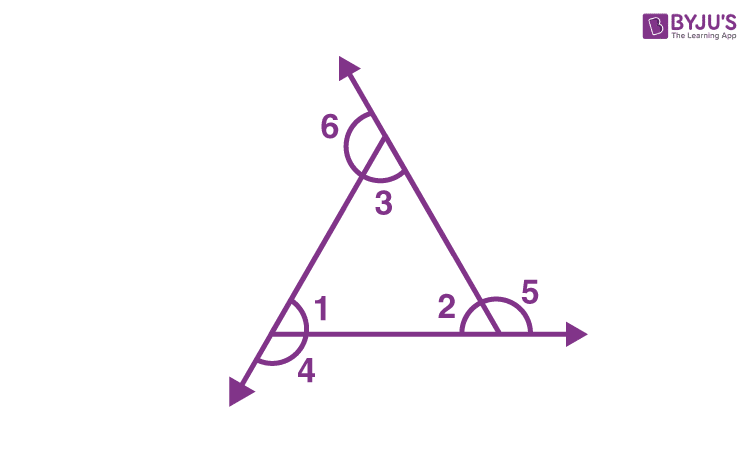
0 0 Similar questions Find theRatios and Proportions Questions & Answers for AIEEE,Bank Exams,CAT,GATE, Bank Clerk,Bank PO The ratio of the angles of a triangle is 3 4 5 The three angles of a quadrilateral is equal to three angles of this triangle What is the sum ofThe angles of a triangle are in the ratio 3 4 5 The measure of the largest angle of the triangle is A) 60° B) 75° C) 1° D) 150° Correct Answer B) 75° Description for Correct answer Ratio of angles = 3 4 5 \( \Large (345)\ unit=180 ^{\circ} \) \( \Large 12\ units=180 ^{\circ} \) \( \Large 1unit=\frac{180 ^{\circ}}{12}=180 ^{\circ} \) Part of solved Mensuration questions and

Are The Trianfle Similar If They Are Identify The Similarity Ratio Yes The Similarity Ratio Is Brainly Com
Triangle with ratio of 3 to 4 to 5
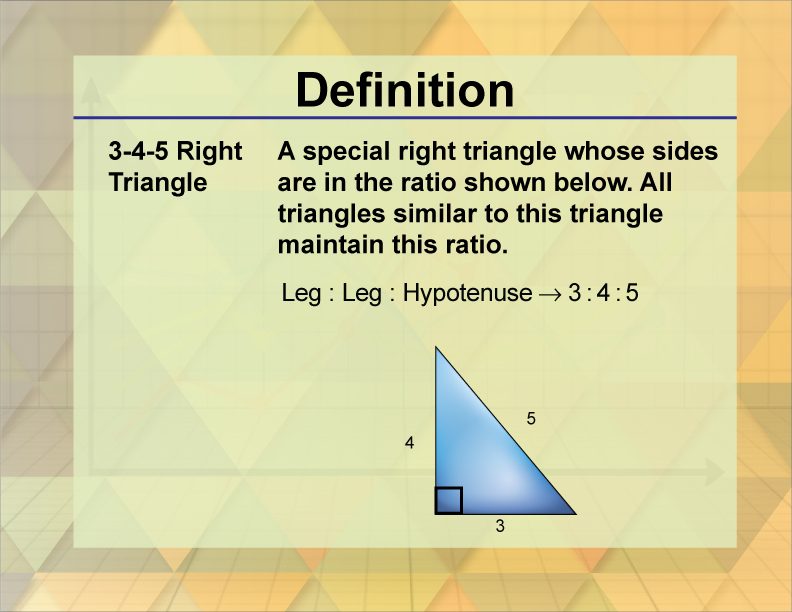
Triangle with ratio of 3 to 4 to 5-Step 1 Add all the terms in the ratio EXAMPLE 3 4 5 = 12Step 2 Divide this sum by each term in the ratio EXAMPLE;A 345 right triangle is a triangle whose side lengths are in the ratio of 345 In other words, a 345 triangle has the ratio of the sides in whole numbers called Pythagorean Triples In other words, a 345 triangle has the ratio of the sides in whole numbers called Pythagorean Triples
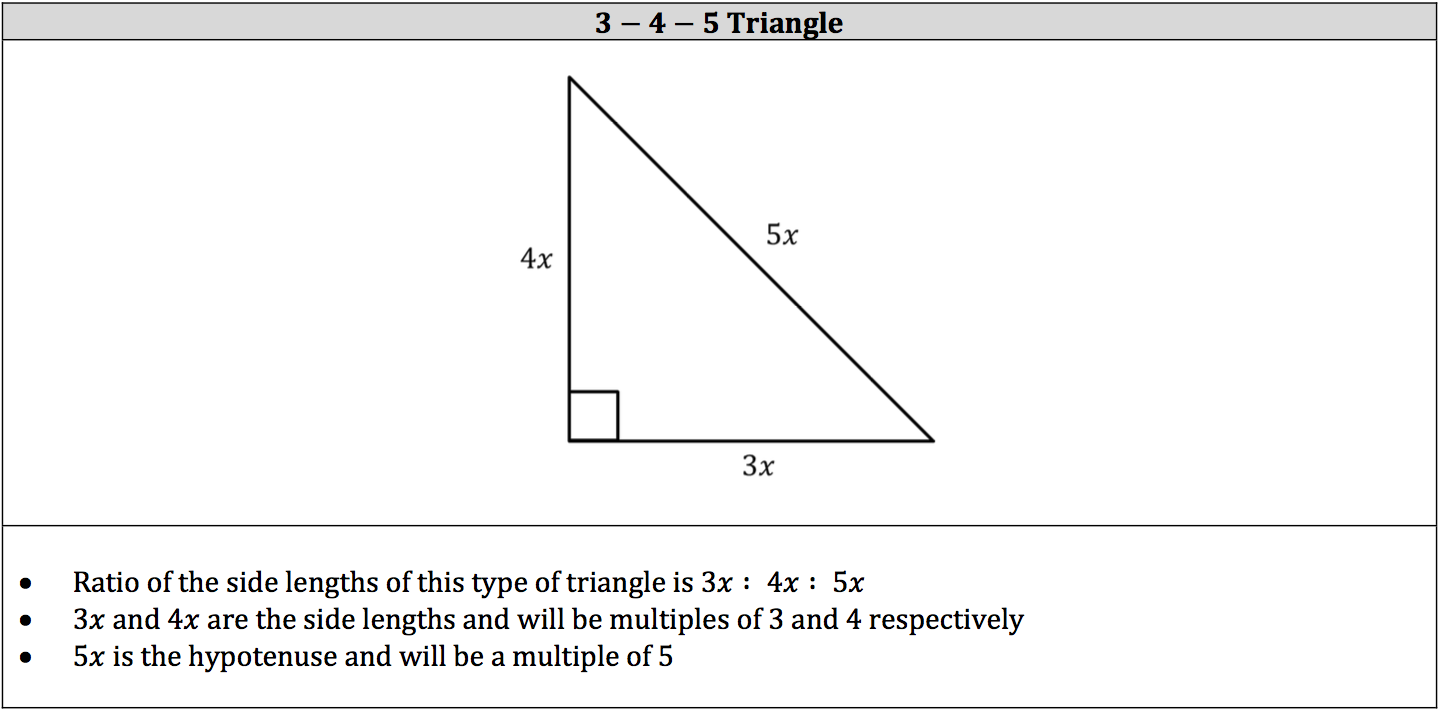



3 4 5 Triangle Piqosity Adaptive Learning Student Management App
The ratio of the angles of a triangle is 345find the measure of each angleA) 225 cm, 30 cm, and 375 cm B) 193 cm, 257 cm, and 321 cm C) 75 cm, 115 cm, and 321 cm D) 105 cm, 115 cm, and 125 cmIf we substitute the numbers from a 345 triangle into this formula, we then have 9″ 16″ = 25″ Remembering the 345 Using triangle dimensions of 3, 4, and 5 is easy to remember and deploy There are no difficult equations to remember and the 345 method will always produce a perfect right angle very time
And, the ratio of the perimeter will be consistent with the sides perimeter 86 units area 3 sq units Since K and S are fight angles, they are congruent"The sides of a triangle are in the ratio 3 4 5 The measure of the largest angle of the triangle is `60^0`b `75^0`c `1^0`d `150^0`"Click here👆to get an answer to your question ️ The angles of a triangle are in the ratio 345 Find the smallest angle
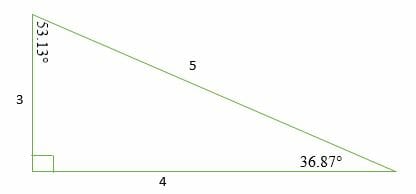
Angles of a triangle are in the ratio 3 4 5 Find the angles Medium Open in App Solution Verified by Toppr Angles are in the ratio of 3 4 5 Let the angles be 3 x, 4 x, 5 x ∴ 3 x 4 x 5 x = 1 8 0Sum of the angles of triangle are 1 8 0 o ∴ 1 2 x = 1 8 0 ∴ x = 1 5 Hence, the angles are 4 5 ∘, 6 0 ∘, 7 5 ∘ Was this answer helpful? Perimeter of a triangle = abc Here given the ratio 345 The sides are 3x,4x,5x 3x4x5x = 90 12x = 90 12x/12 = 90/12 x = 75cm First side of triangle = 3x = 3*75 = 225cm Second side of triangle = 4x = 4*75 = 30 cm Third side of triangle = 5x = 5*75 =375 cmIn other words, a 345 triangle has the ratio of the sides in whole numbers called Pythagorean Triples This ratio can be given as Side 1 Side 2 Hypotenuse = 3n 4n 5n = 3 4 5 We can prove this by using the Pythagorean Theorem as follows ⇒ a 2 b 2 = c 2 ⇒ 3 2 4 2 = 5 2 ⇒ 9 16 = 25 25 = 25 A 345 right triangle has the three internal angles as 3687 °, 5313 °, and 90



Getting Square With The 3 4 5 Triangle



Construct A Triangle With A Given A Perimeter In The Ratio 2 3 4 Technical Graphics
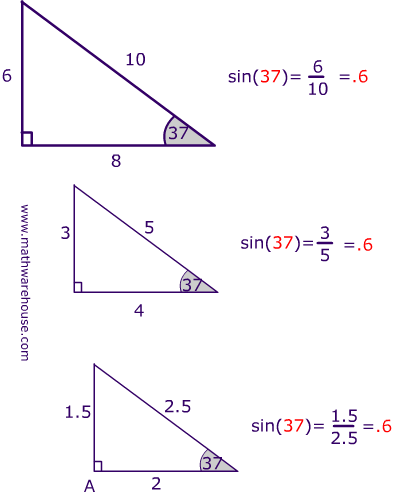
3 The triangle area using Heron's formula Heron's formula gives the area of a triangle when the length of all three sides is known There is no need to calculate angles or other distances in the triangle first Heron's formula works equally well in all cases and types of triangles 4 Calculate the heights of the triangle from its area There are many ways to find the height of the triangle The ratios of corresponding sides are 6/3, 8/4, 10/5 Finally, What is the ratio of the sides of a right triangle?, For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90° This is called an "anglebased" right triangleAny triangle whose sides are in the ratio 345 is a right triangle Such triangles that have their sides in the ratio of whole numbers are called Pythagorean Triples There are an infinite number of them, and this is just the smallest See pythagorean triples for more information If you multiply the sides by any number, the result will still be a right triangle whose sides are in the ratio 3



3 4 5 Golden Ratio



Special Right Triangles And Ratios Geometry
3) 4) 5) Statements A B C = 180 DEF= 180 Reasons 1) Given 2) Sum of interior angles of triangle is 180 degrees 3) Subtraction 4) Subtstitution 5) Substitution c c c 180 180 180 The ratios of the coresponding sides will be equal;The intercept theorem, also known as Thales's theorem, basic proportionality theorem or side splitter theorem is an important theorem in elementary geometry about the ratios of various line segments that are created if two intersecting lines are intercepted by a pair of parallelsIt is equivalent to the theorem about ratios in similar triangles 345 triangle does not mean that the ratios are always exactly 3 4 5 But, it can be any factor of numbers, keeping the basic ratio of the three sides the same Few other examples of 345 triangles are 6810;



The 3 4 5 Triangle




3 4 5 Triangle
Answer (1 of 3) Let the angles A, B and C of the triangles be 3x, 4x and 5x 3x4x5x = 180 12x= 180 x = 15 A= 3(15)= 45 = π/4 B= 4(15) = 60 = π/3 C= 5(15)= 75 = 5π/12 Let a, b and c be the sides of the triangle opposite to A, B and C respectively Longest side C= Side opposite to largest(Algebra II) The sides of a triangle are in the ratio 3 4 5 What is the length of each side if the perimeter of the triangle is 90 cm?Therefore, a triangle having sides whose ratios are 345 is a right triangle Again, let's assume that we have a 345 triangle that has sides actually 3 cm, 4 cm, and 5 cm in length That means its perimeter would be cm But the problem says that you have a triangle with a perimeter of 144 cm Therefore, the given triangle has a perimeter that is 12 times greater than the perimeter of the




The Sides Of A Triangle Are In The Ratio 3 4 5 The Measure Of The Largest Angle Of The Triangle Youtube
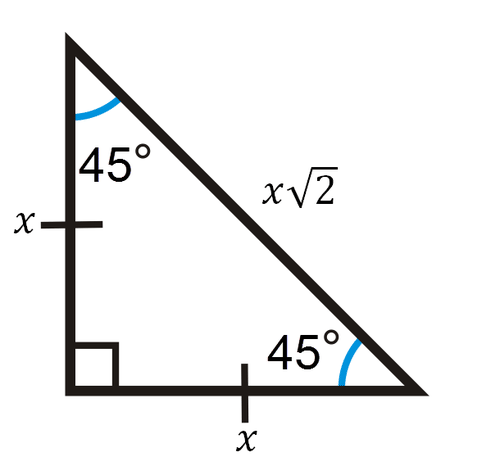



Special Right Triangles Read Geometry Ck 12 Foundation
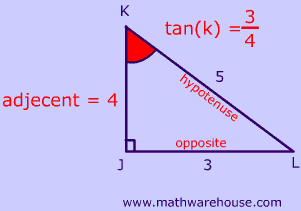
345 Right Triangle A 345 triangle is right triangle whose lengths are in the ratio of 345 When you are given the lengths of two sides of a right triangle, check the ratio of the lengths to see if it fits the 345 ratio Side1 Side2 Hypotenuse = 3n 4n 5n Solve problems with 345 right triangles Example 1The total angle of a triangle is 180 degrees We can simply add the values of the ratios (245=11), then divide 180 by 11, to get 1636 degress Then you can multiply 1636 by each ratio needed (1636x2, 1636x4, and 1636x5), to get the measurements ofPythagorean Triples A right triangle where the sides are in the ratio of integers (Integers are whole numbers like 3, 12 etc) For example, the following are pythagorean triples There are infinitely many pythagorean triples There are 50 with a hypotenuse less than 100 alone Here are the first few 345 , 6810 , , , 815
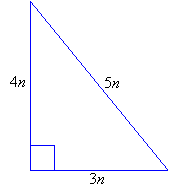



3 4 5 Right Triangles Worked Solutions Examples Videos




If The Sides Of A Triangle Are In The Ratio 3 4 5 And The Perimeter Of The Triangle Is 72 Inches What Are The Lengths Of The Sides Study Com
Thus, the sides are 5 x 15, 3 x 15 and q x 15 That is the sides are 75m, 45m and 60m Since the sides are in the ratio, 5 3 4, it is a Pythagorean triplet, Therefore, the triangle is a rightangled triangle, Area of a rightangled triangle = `1/2` x base x altitude ⇒ `1/2` x 45 x 60 ⇒ 45 x 30 = 1350 m 2 (ii) Consider the following figure Example 26 1 Express the ratio 12 feet to 48 feet in reduced form Solution 12 feet to 48 feet = 12 feet 48 feet = 12 ÷ 12 48 ÷ 12 R e d u c e = 1 4 Answer 1 to 4 If the units are different, then we must be sure to include them because the ratio represents a rateThe angles of a triangle are in the ratio 345 Find the smallest angle in degrees and the greatest angle in radians



Special Right Triangle 30 60 45 45 37 53 Elearning




The Sides Of A Triangle Are In The Ratio 3 4 5 The Measure Of The Largest Angle Of The Triangle Brainly In
Other Combinations Yes, there are other The 345 triangle is the best way I know to determine with absolutely certainty that an angle is 90 degrees This rule says that if one side of a triangle measures 3 and the adjacent side measures 4, then the diagonal between those two points must measure 5 in order for it to be a right triangle Confused yet?\frac{3}{12}, \frac{4}{12}, \frac{5}{12}Step 3 Multiply the fraction with the given perimeter To find triangle sides \frac{3}{12}* 30 = 75 \frac{4}{12}* 30 = 10 \frac{5}{12}* 30 = 125 Method 2Step 1 Assume common ratio as x NOTE We know that there is a common ratio




3 4 5 Right Triangles Explanation Examples
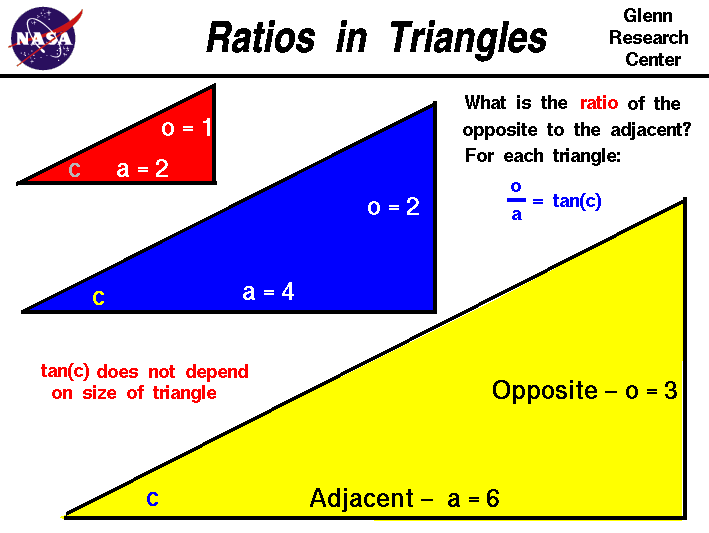



Ratios In Triangles
The sides of the triangle are in the ratio 3 4 5 and its perimeter is 48cm Find the perimeter of a triangle whose vertices are the midpoints of the sides of this triangle We denote the lengths of the sides of the triangle through 3 * x, 4 * x, 5 * x, then 3 * x 4 * x 5 * x = 48 12 * x = 48 X = 4 Then the lengths of the sides are 3 * 4 = 12, 4 * 4 = 16, 5 * 4 = Since the In a given triangle , its sides are in the ratio of 3 4 5 Let us assume that these sides are 3x, 4x and 5x respectively Perimeter > 3x 4x 5x > 12 x But, the perimeter is given as 144 cm So 12 x = 144 > x = 12 Side 1 = 3x = 3 * 12 = 36 cm Side 2 = 4x = 4 * 12 = 48 cm Side 3 = 5x = 5 * 12 = 60 cm Using Herons FormulaKCET 06 If the angles of a triangle are in the ratio 3 4 5, then the sides are in the ratio (A) 345 (B) 2√3√31 √2√6√31 (D)




Q3 The Angles Of A Triangle Ar Lido




The 3 4 5 Triangle Ssdd Problems
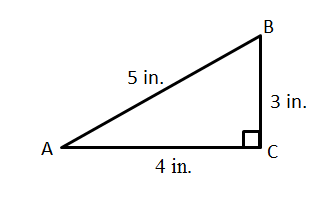
3) 5 2 = 25, so the 3 4 5 right triangle ratio is satisfied Let's prove it again with a different example We are going to multiply the numbers of the ratio by a common factor of 2 1) 6 2 8 2 = 36 64 = 100 2) 10 2 = 100, so the 3 4 5 right triangle ratio is satisfied 3) This proves the ratio holds true even when scaled by a commonHere are the formulas for these six trig ratios Given a triangle, you should be able to identify all 6 ratios for all the angles (except the right angle) Let's start by finding all 6 ratios for angle A Notice that the csc, sec, and cot can be found simply by flipping the ratio they are associated with Or, you can use the formulas To find the 6 ratios for angle B, just start over again and Think of 345 as a ratio As long as the lengths of the triangle's sides are in the ratio of 345, then it's really a 345 triangle, and all the same rules apply




Square In 3 4 5 Triangle Mind Your Decisions



1
What is the measure of each angle?45, 60, 75The measures of the angles of a triangle are in the ratio 345 What is the measure of each angle?Algebra Rational Equations and Functions Rational Equations Using Proportions 1 Answer MeneerNask Let's call the angles #3x,4x and 5x# They must add up to #180^o# in a triangle, so #3x4x5x=12x=180>x=180//12=15# So the angles are #3*15=45^o# #4*15=60^o# #5Answer (1 of 4) The total angles of a triangle are 180 degrees If all the Three angles are in the ratios of 345, then the angles are in degrees as follows 345= 12 parts of 180 is 15 degrees And the first angle 3/12 or 153 = 45 degrees, the second one is 415 = 60 degrees and the third
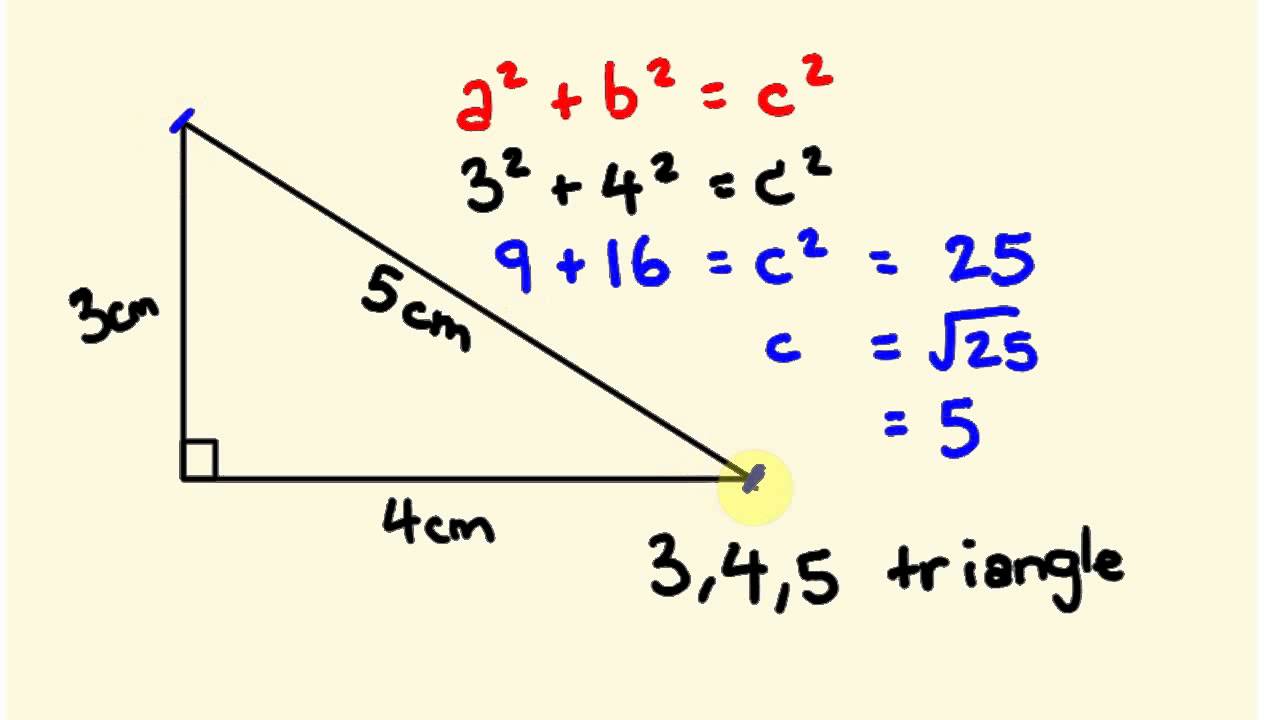



Pythagorus Theorum Math Lesson 3 4 5 Triangle Youtube




Pythagorean Theorem B2 C2 Reem Alabdulkarim Ppt Download
Related to the basic 345 triangle are all triangles whose sides are in the ratio 3 to 4 to 5 but are longer (proportionately) than these basic lengths For example, the triangle pictured in figure 196 is a 34 5 triangle Figure 1916Triangle with sides which are multiples of 3, 4, and 5Properties All three sides are unequal, having a ratio of 3 4 5 (3x 4x 5x for Side 1 side 2 hypotenuse) All three internal angles areGiven, the angles of a triangle are in the ratio 3 4 5 Let the angles be 3x, 4x and 5x Sum of angles of a triangle = 180° ⇒ 3x 4x 5x = 180° ⇒ 12x = 180° ⇒ x = 15° Smallest angle = 3x = 45° Related Questions यदि त्रिभुज के कोण 3 4 5 के अनुपात में हैं, तो




The Angles Of A Triangle Are In The Ratio 3 4 5 Find The Smallest Angle In Degrees And The Greatest Angle In Radians




The Semi Perimeter Of A Triangle Is 96 Cm And Its Sides Are In The Ratio 3 4 5 Find The Area
The ratio of the side of the triangle = 3 ∶ 4 ∶ 5 The perimeter of the triangle = 24 cm Concept used The perimeter of triangle = sum of the length of all the sides Area of triangle = (1/2) × base × height Calculations Let the sides of the triangle be 3x, 4x and 5x ⇒ 3xGet answer The sides of a triangle are in the ratio 3 4 5 The measure of the largest angle of the triangle is 60^0 b 75^0 c 1^0 d 150^0 The sides of a triangle `ABC` are in the ratio `345` If the perimeter of triangle `ABC` is `60,` then its lengths of sides are class11;



3 4 5 Right Triangles Explanation Examples




Special Right Triangle Wikipedia
Share It On Facebook Twitter Email 1 Answer 0 votes answered The angles of a triangle are in the ratio 345 How do you find the measures of the angles? But the 345 triangle is the layman's substitute for the Pythagorean theorem The 345 triangle is the best way I know to determine with absolutely certainty that an angle is 90 degrees This rule says that if one side of a triangle measures 3 and the adjacent side measures 4, then the diagonal between those two points must measure 5 in




The Ratio Of The Sides Of Triangle Ebd To The Sides Of Triangle Abc Is 3 4 Calculate The Side Lengths Of Triangle Abc Study Com




3 4 5 Triangle Angles Sides How To Solve Full Lesson
It could be 3 mm, 3 inches, 3 feet or 3 miles It doesn't matter theTheCutePrincess630 RATIO OF ANGLES OF A TRIANGLE = 345 LET THE COMMON MULTIPLE BE x 1st angle = 3×x = 3x 2nd angle = 4×x = 4x 3rd angle = 5×x = 5x ATP 1st angle 2nd angle 3rd angle = 180⁰ Sum of all angles of a triangle is 180⁰ = 3x 4x 5x = 180⁰ = 12x = 180⁰ => x = 180/12 => x = 15 Therefore, 1st angle = 3x = 3×15 = 45⁰ 2nd angle = 4x = 4×15 = 60⁰ 3rdThis triangle has the ratio 6810, which is proportionate to 345, so it is a 345 right triangle How to Use the Pythagorean Theorem Practical Uses of 345 Triangles




3 4 5 Triangle Calculator Right Triangle Calculator Right Triangle Solver Special Triangles Right Triangle Pythagorean Triple Triangle



Pictures Of 3 4 5 Right Triangles Free Images That You Can Download And Use
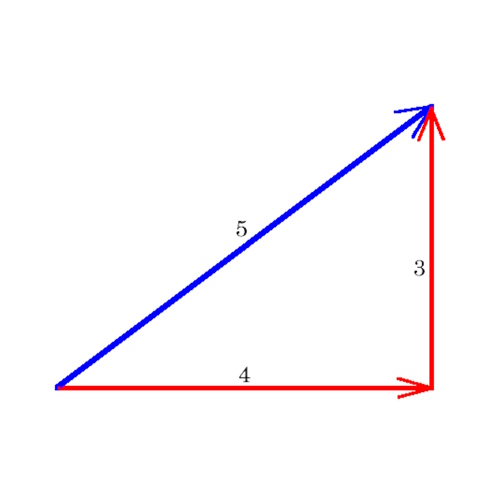
Send forsale 732 10 months ago 3 0 Between 3 and 4 obviously Send You might be interested in decide if the following change is an increase or decrease then determine the percent of change 48 inches to 30 inches Wewaii 24 48 inchesAnd you have your "3,4,5" triangle with its right angle The Mathematics Behind It The Pythagoras Theorem says In a rightangled triangle, the square of a (a 2) plus the square of b (b 2) is equal to the square of c (c 2) a 2 b 2 = c 2 Let's check if it does work 3 2 4 2 = 5 2 Calculating this becomes 9 16 = 25 Yes, it works !



1



What Is The Value Of Cos 53 Quora



The Lengths Of The Sides Of A Triangle Are In The Ratio 4 5 3 And Its Perimeter Is 96 Cm Find Its Area Sarthaks Econnect Largest Online Education Community




If The Sides Of A Triangle Be In The Ratio 2 3 4 The Ratio Of The Corresponding Altitudes Is A 6 5 3 B 4 5 6 C 5 4 3 D 6 4 3




The Golden Ratio In Amalgam Of 1 2 5 Triangle And 3 4 5 Triangle Download Scientific Diagram




The Sacred Triangle 3 4 5 Sacred Geometry Symbols Sacred Sacred Geometry




The Golden Ratio In Amalgam Of 1 2 5 Triangle And 3 4 5 Triangle Download Scientific Diagram



The 3 4 5 Triangle




Golden Ratio In Geometry



3 4 5 Right Triangles Explanation Examples




Getting Square With The 3 4 5 Triangle



The 3 4 5 Triangle



Definition Triangle Concepts 3 4 5 Right Triangle Media4math




Are The Trianfle Similar If They Are Identify The Similarity Ratio Yes The Similarity Ratio Is Brainly Com
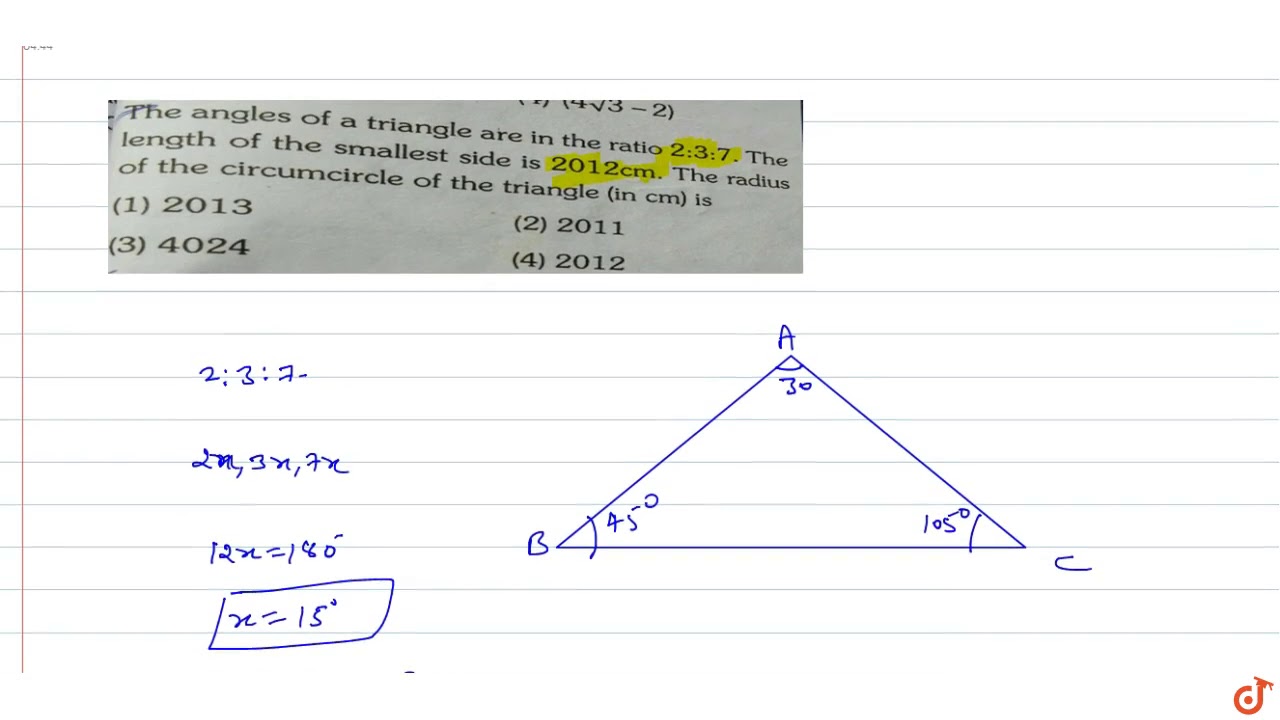



The Angle The Angles Of A Triangle Are In The Ratio 2 3 7 Thelength Of The Smallest Side Is Youtube




Conquering Right Triangles The Pythagorean Theorem On Act Math Part 1 Magoosh Blog High School




The Golden Ratio 3 4 5 Bob Krueger Brilliant




The Golden Ratio In Amalgam Of 1 2 5 Triangle And 3 4 5 Triangle Download Scientific Diagram
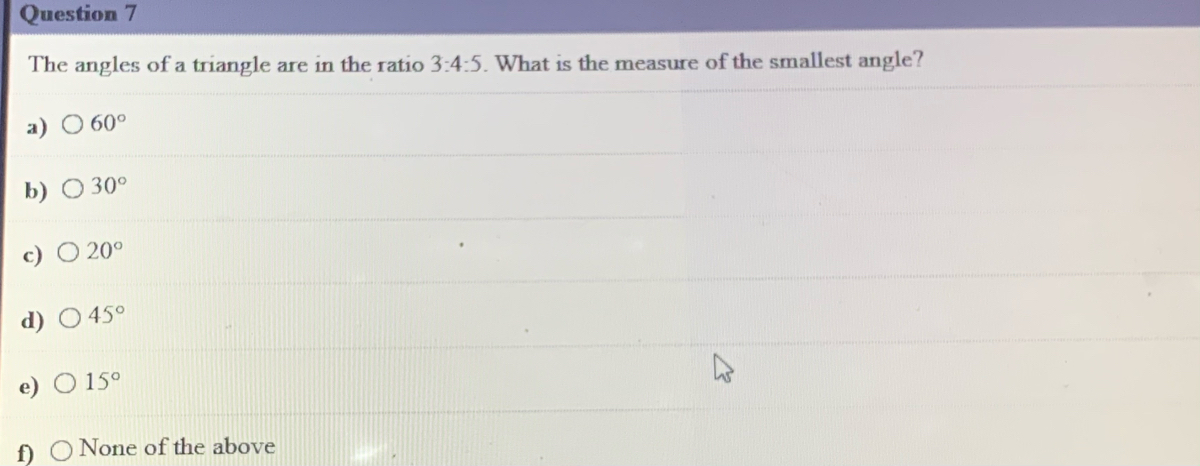



Answered Question 7 The Angles Of A Triangle Are Bartleby



If The Length Of The Sides Of A Triangle Are In The Ratio Of 4 5 6 And The Inradius Of The Triangle Is 3 Cm What Is The Altitude Of The Triangle Corresponding
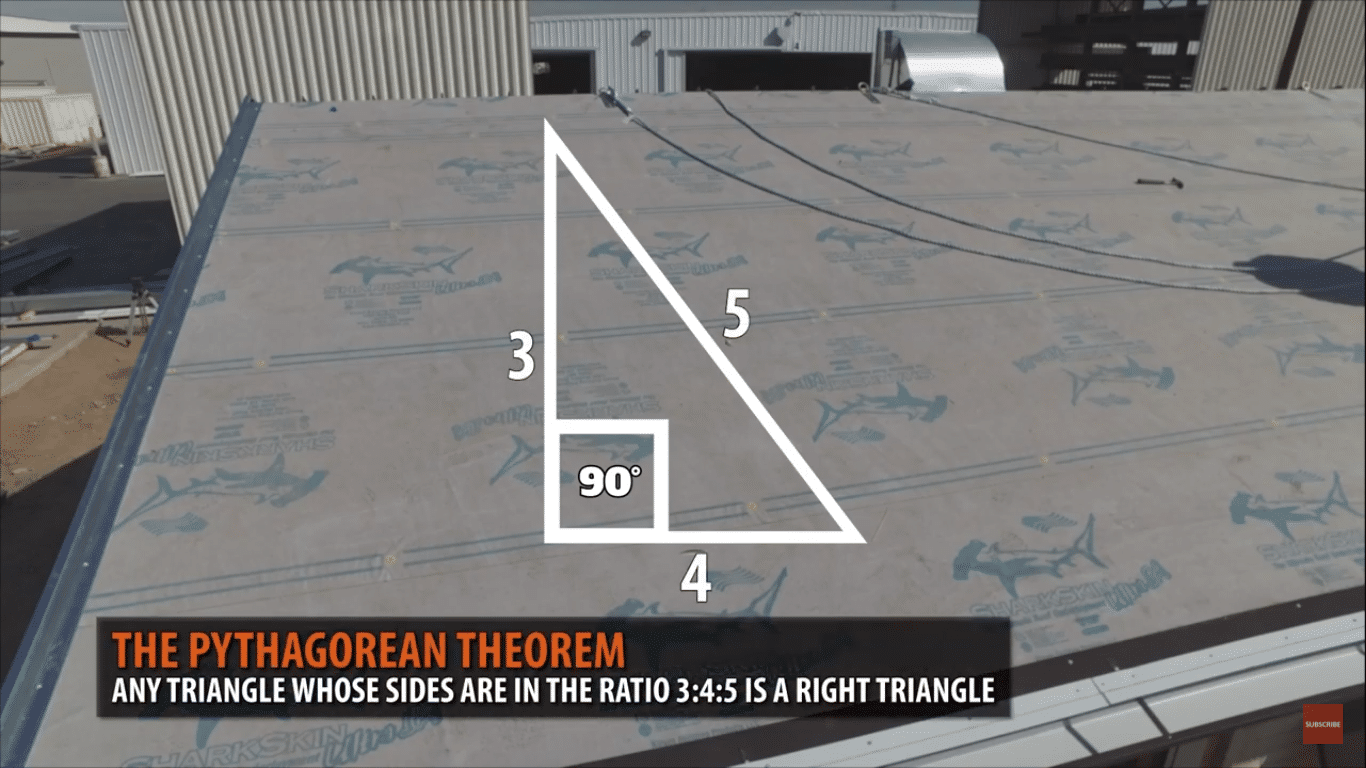



How To Square A Metal Roof The 3 4 5 Triangle Method




Properties Of 3 4 5 Triangles Definition And Uses Video Lesson Transcript Study Com




3 4 5 Triangle




The Lengths Of The Sides Of A Triangle Are In The Ratio 4 5 3 And Its Perimeter Is 96 Cm Find Its Area




The Angles Of A Triangle Are In The Ratio 3 5 4 Calculate The Size Of Each Angle Brainly In




3 4 5 Right Triangles Explanation Examples




Pythagorean Triangle With Side Lengths Having The Ratio 3 4 5 The Download Scientific Diagram




3 4 5 Triangle Piqosity Adaptive Learning Student Management App
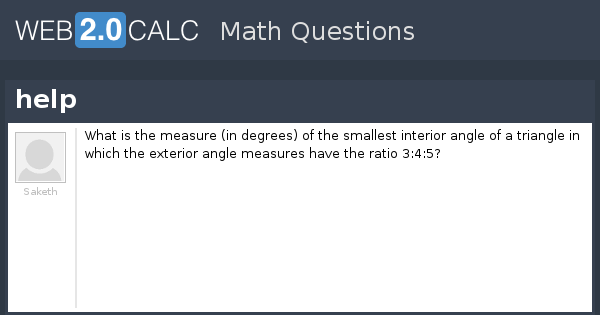



View Question Help




The Angles Of A Triangle Are In The Ratio 3 4 5 Find The Smallest Angle In Degrees And The Youtube
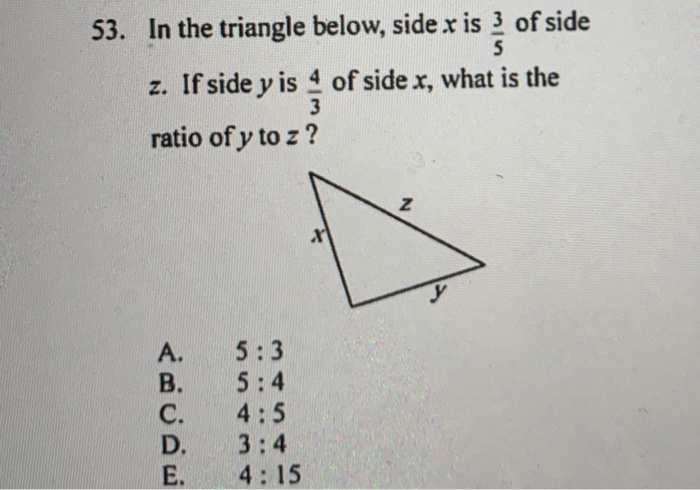



53 In The Triangle Below Side X Is 3 Of Side Z If Chegg Com
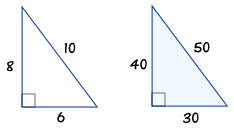



3 4 5 Triangle



1




3 4 5 Triangle Angles Sides How To Solve Full Lesson




3 4 5 Triangle Angles Sides How To Solve Full Lesson




The Sides Of A Triangle Abc Are In The Ratio 3 4 5 If The Perimeter Of Triangle Abc Is 60 Then Its Lengths Of Sides Are




Median Don Steward Mathematics Teaching Triangle Angles In A Ratio




Using Similarity To Estimate Ratio Between Side Lengths Video Khan Academy




Resources 3 4 5 Principle



What Are Sides Ratio A Triangle Whose Angle Ratio Are 1 2 3 Quora
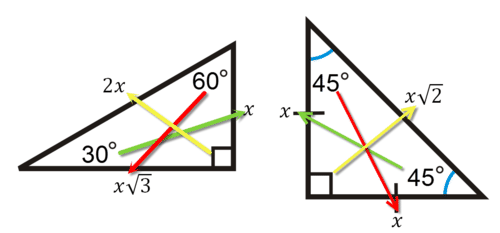



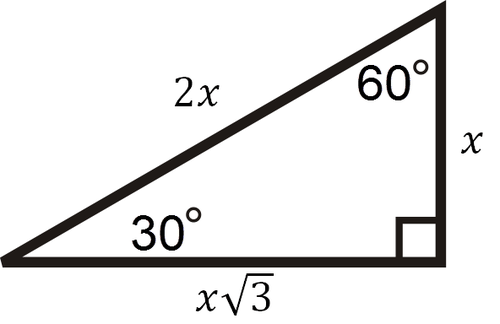
Special Right Triangles Ck 12 Foundation




African Creation Energy The Ptah Horus Pythagoras Theorem The African Origin Of The Pythagorean Theorem




Match The Trig Function With The Correct Ratio Given Chegg Com



Cosecant Cosecant Function Csc



1




Bellringer Solve For Y 1 Y 5 5 2 Y 7 Ppt Download



Solved Find The Cosine Ratio Of Angle Hint Use The Slash Symbol To Represent The Fraction Bar And Enter The Fraction With No Spaces Pict Course Hero




Special Right Triangle Wikipedia




Manasataramgini A Simple Construction To Get Various Vulgar Fractions The Golden Ratio And The 3 4 5 Triangle Some Believe It Might Have Been Used By Ancients In Temple Construction And To




Construct A Triangle Mnp Whose Perimeter Is 15 Cm And Whose Sides Are In The Ratio 2 3 4
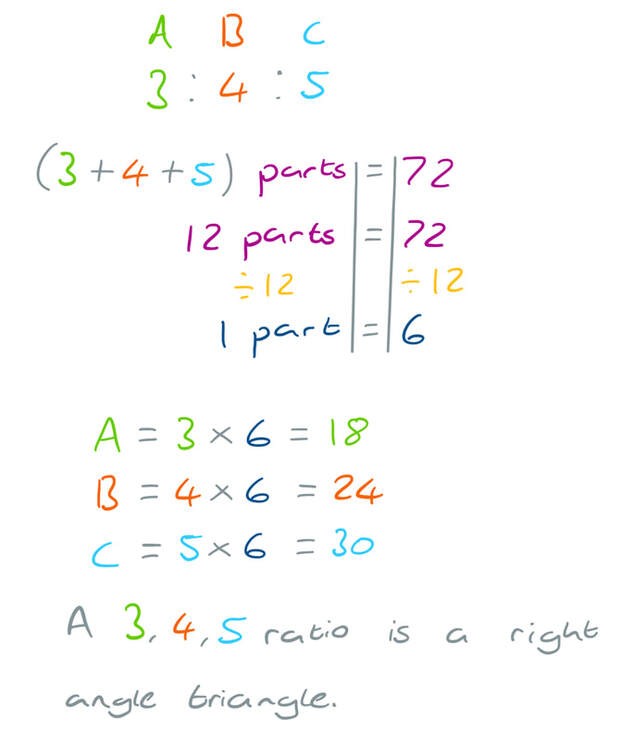



Q8 Answers Paper 1 June 18 Edexcel Gcse Maths Higher Elevise



A Thing Or Two About 3 4 5 Triangle Angles Get Education



Sine Cosine And Tangent Ratios Of A Triangle How To Write The Trig Ratios Of Right Triangles



The 6 Trig Ratios




Old Stuff Will Be Used In This Section Triangle Sum Theorem The Sum Of The Measures Of The Angles In A Triangle Is 180 Pythagorean Theorem Ppt Download




The Angles Of A Triangle Are In The Ratio 3 4 5 Find The Smallest Angle In Degree And The Greatest Angle In Radians




Special Right Triangles 3 4 5 Triangle Study Com



3 4 5 Golden Ratio




3 4 5 Triangle Piqosity Adaptive Learning Student Management App
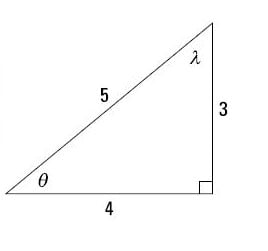



Use 6 Different Ratios Of A Right Triangle Dummies
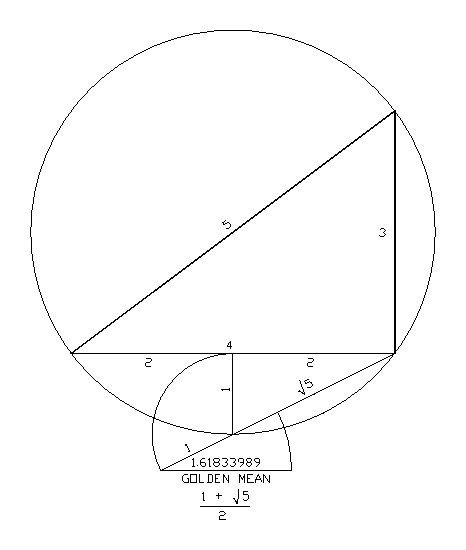



The 3 4 5 Right Triangle And The Golden Mean




Finding Triangle Angles In A 2 3 4 Ratio Youtube




Math Example Ratios And Rates Example 12 Media4math
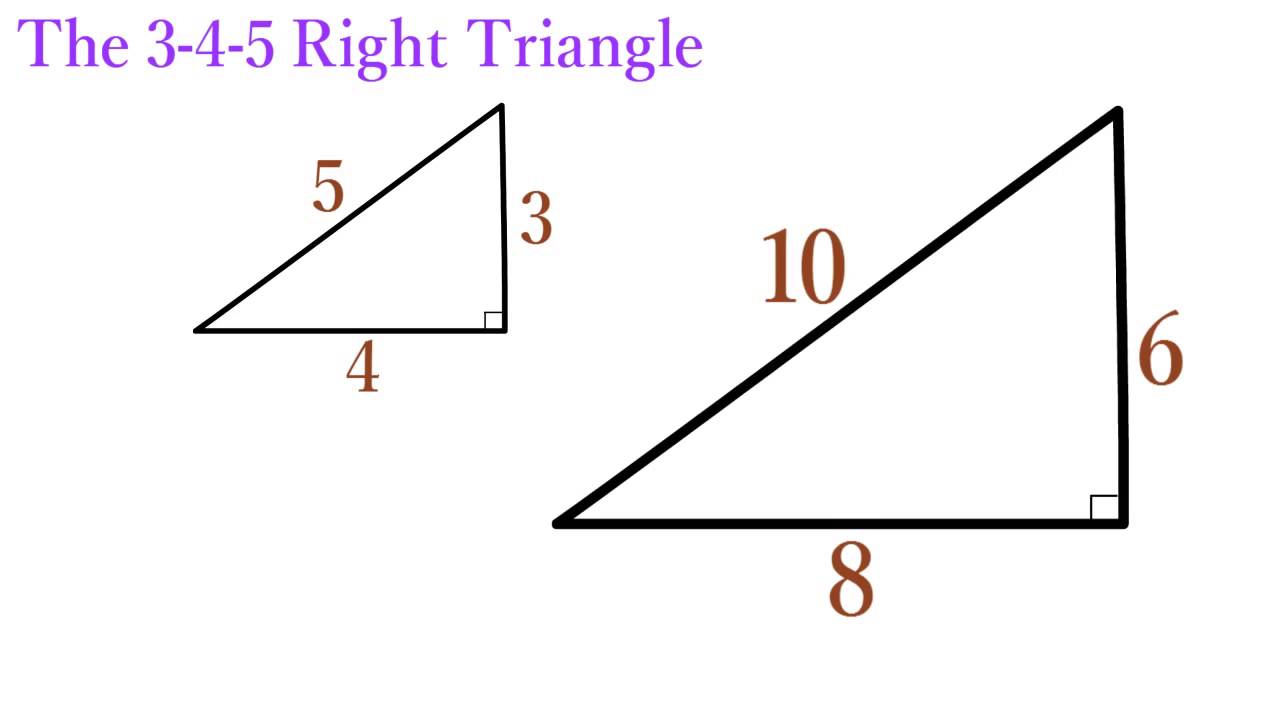



Lesson 12 The 3 4 5 Right Triangle Simplestep Learning Youtube



Solution Hi I 39 M Having A Bit Of Trouble Do You Think You Could Help The Angles Of A Triangle Are In The Ratio 3 4 5 If The Shortest Side Has A Length Of



Construct A Triangle Abc Whose Perimeter Is 13 Cm And Whose Sides Are In The Ratio 3 4 5 Quora




Solved Use An Algebraic Equation To Solve The Problem The Chegg Com
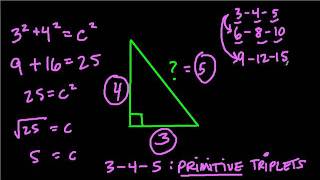



3 4 5 Right Triangles Worked Solutions Examples Videos




3 4 5 Triangle Definition Math Open Reference




The Ratio Of The Measures Of The Angels In A Triangle Chegg Com




In The Triangle Below 4 5 Represents Which Ratio Brainly Com



What Are The Angle Measurements Of A 3 4 5 Right Triangle Quora
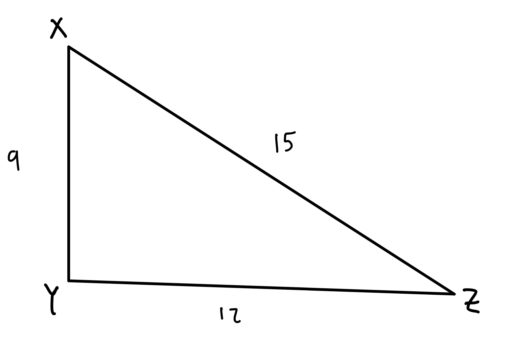



2d Shapes Right Triangles
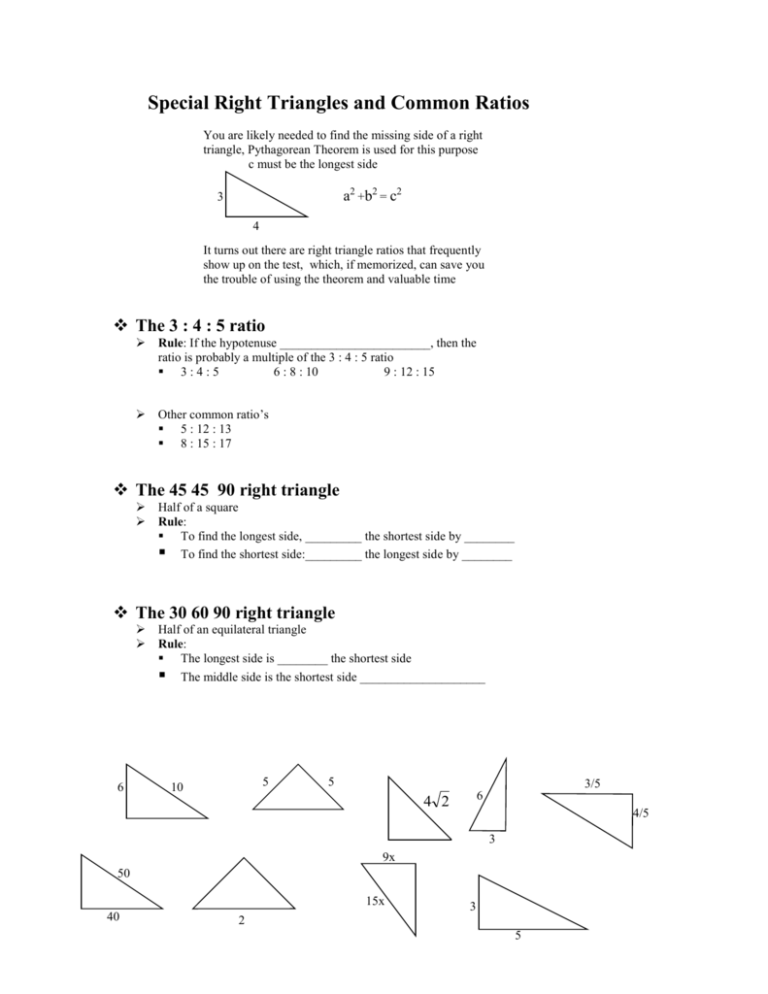



Special Right Triangles And Common Ratios




The Sine Function Selraybob




3 4 5 Triangle Definition Math Open Reference


